Planar Face Transform

Here is another contribution by Joe Offord of Enclos ↗, who already shared valuable insights on accessing curtain wall geometry, speeding up the interactive selection process, mirroring in a new family and changing the active view.

Above all, he implements all his stuff in VB, so this is also something for you VB aficionados.

This time, Joe looks at a command that redraws a planar face’s edges in a drafting view. The issue is somewhat related to the discussion of polygon transformations.

However, instead of using rotations and translations, which can be difficult to determine in 3D, Joe wrote a utility function that re-maps the global coordinate system to the planar face’s coordinate system using vectors and origins.

The command prompts the user to select a planar face on an elements, creates a new drafting view, retrieves the edges of the selected face, and transforms them from the 3D space to the drafting view.

To test this, I selected the following slightly lopsided wall in 3D:

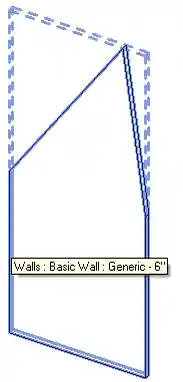
The command generated a new drafting view showing the wall profile edges like this:

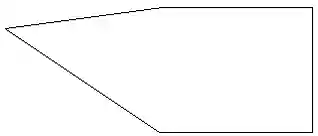
Here is the Execute method implementation for the mainline of the command:

  Public Function Execute( _
    ByVal commandData As ExternalCommandData, _
    ByRef message As String, _
    ByVal elements As ElementSet) As Result Implements IExternalCommand.Execute
 
    Dim uiapp As UIApplication = commandData.Application
    Dim app As Application = uiapp.Application
    Dim uidoc As UIDocument = uiapp.ActiveUIDocument
    Dim doc As Document = uidoc.Document
    Dim sel As Selection = uidoc.Selection
 
    Try
      Dim ref As Reference = sel.PickObject( _
        ObjectType.Face, "Select a face")
 
      Dim elem As Element = doc.GetElement(ref)
 
      Dim gObj As GeometryObject _
        = elem.GetGeometryObjectFromReference(ref)
 
      Dim face As PlanarFace = TryCast(gObj, PlanarFace)
 
      If face Is Nothing Then
        MsgBox("Not a planar face")
      End If
 
      Dim v As ViewDrafting = Nothing
 
      Dim tr As New Transaction(doc, "Draw Face")
      tr.Start()
 
      Try
        v = doc.Create.NewViewDrafting 'create a new view
        v.Scale = 48 '1/4" = 1'-0"
 
        'this transform re-orients the global 
        'coordinate system to the face's coordinate system
        Dim trans As Transform _
          = Util.PlanarFaceTransform(face)
 
        For Each eArr As EdgeArray In face.EdgeLoops
          For Each e As Edge In eArr
            Dim c As Curve = e.AsCurveFollowingFace(face)
            c = c.Transformed(trans) 'orient the curve on the XY plane
            doc.Create.NewDetailCurve(v, c) 'draw the curve
          Next
        Next
 
        tr.Commit()
      Catch ex As Exception
        tr.RollBack()
        MsgBox("Error: " + ex.Message)
      End Try
 
      If tr.GetStatus = TransactionStatus.Committed Then
        uidoc.ActiveView = v
      End If
 
    Catch ex As Exception
      MsgBox("Error: " + ex.Message)
    End Try
 
    Return Result.Succeeded
 
  End Function

The transformation from the planar face coordinate system is created by the following two utility methods:

  ''' <summary>
  ''' Return a transform that changes a x,y,z 
  ''' coordinate system to a new x',y',z' system
  ''' </summary>
  Public Shared Function TransformByVectors( _
    ByVal oldX As XYZ, _
    ByVal oldY As XYZ, _
    ByVal oldZ As XYZ, _
    ByVal oldOrigin As XYZ, _
    ByVal newX As XYZ, _
    ByVal newY As XYZ, _
    ByVal newZ As XYZ, _
    ByVal newOrigin As XYZ) As Transform
 
    ' [new vector] = [transform]*[old vector]
    ' [3x1] = [3x4] * [4x1]
    '
    ' [v'x]   [ i*i'  j*i'  k*i'  translationX' ]   [vx]
    ' [v'y] = [ i*j'  j*j'  k*j'  translationY' ] * [vy]
    ' [v'z]   [ i*k'  j*k'  k*k'  translationZ' ]   [vz]
    '                                               [1 ]
    Dim t As Transform = Transform.Identity
 
    Dim xx As Double = oldX.DotProduct(newX)
    Dim xy As Double = oldX.DotProduct(newY)
    Dim xz As Double = oldX.DotProduct(newZ)
 
    Dim yx As Double = oldY.DotProduct(newX)
    Dim yy As Double = oldY.DotProduct(newY)
    Dim yz As Double = oldY.DotProduct(newZ)
 
    Dim zx As Double = oldZ.DotProduct(newX)
    Dim zy As Double = oldZ.DotProduct(newY)
    Dim zz As Double = oldZ.DotProduct(newZ)
 
    t.BasisX = New XYZ(xx, xy, xz)
    t.BasisY = New XYZ(yx, yy, yz)
    t.BasisZ = New XYZ(zx, zy, zz)
 
    ' The movement of the origin point 
    ' in the old coordinate system
 
    Dim translation As XYZ = newOrigin - oldOrigin
 
    ' Convert the translation into coordinates 
    ' in the new coordinate system
 
    Dim translationNewX As Double _
      = xx * translation.X _
        + yx * translation.Y _
        + zx * translation.Z
 
    Dim translationNewY As Double _
      = xy * translation.X _
        + yy * translation.Y _
        + zy * translation.Z
 
    Dim translationNewZ As Double _
      = xz * translation.X _
        + yz * translation.Y _
        + zz * translation.Z
 
    t.Origin = New XYZ( _
      -translationNewX, _
      -translationNewY, _
      -translationNewZ)
 
    Return t
 
  End Function
 
  Public Shared Function PlanarFaceTransform( _
    ByVal face As PlanarFace) As Transform
 
    Return Util.TransformByVectors( _
      XYZ.BasisX, _
      XYZ.BasisY, _
      XYZ.BasisZ, _
      XYZ.Zero, _
      face.Vector(0), _
      face.Vector(1), _
      face.Normal, _
      face.Origin)
  End Function

Here is PlanarFaceTransform.zip including the complete source code and Visual Studio solution of this command.

Many thanks to Joe for sharing this!